В равнобедренного треугольнике авс угол при вершине В в 2 раза меньше угла при основании,...

Question

В равнобедренного треугольнике авс угол при вершине В в 2 раза меньше угла при основании, АД-биссектриса, Д пренадлежит ВС. Докажите, что треугольник САД и треугольник АДВ равнобедренные. (решите с рисунком)

Comments

АД к чему проведено? к основанию или боковой стороне?

---

Рассматриваем 2 случая и получаем, что А не может быть вершиной при основании --> ВС- основание равнобедр. треуг.

---

Ад проведена к ВС

---

это ясно, надо определить ВС - бок. сторона или основание...ВС - основание!

---

"угол при вершине В в 2 раза меньше угла при основании, " из этого АС - основание

Answer 1

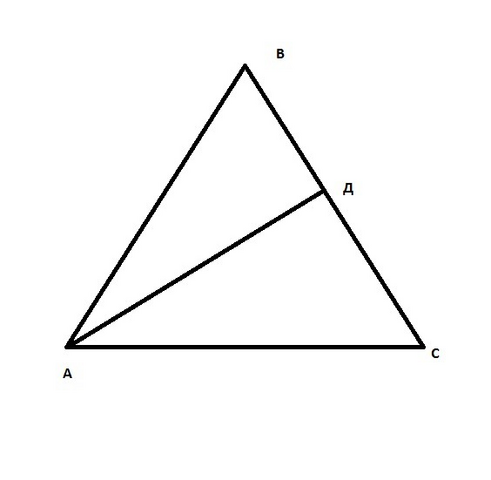
Рассмотрим треугольник АВС - он р/б, углы при основании равны, а сумма всех углов 180*. Мы знаем, что угол при основании в 2 раза больше , чем угол напротив основания.

Пусть х угол В , а углы А и С по 2х.

х+2х+2х=180*

5х=180*

х=180/5

х=36*(угол В)

2х=36*2=72*(углы А и С)

Углы, на которые делит биссектриса угол А, равны 36*(она делит его пополам)

Рассмотрим треугольники АСД и АДВ - нам в них известно в каждом по два угла.

ΔАСД

∠ДАС =36* , ∠АСД=72*

Сумма всех углов в треугольнике 180*.

∠АДС=180-36-72=72*

Если в треугольнике есть два равных угла, то он р/б (∠АСД=72*=∠АДС)

Рассмотрим треугольник АДВ.

Мы уже нашли два равных угла по 36*

В и ДАВ =36*

---