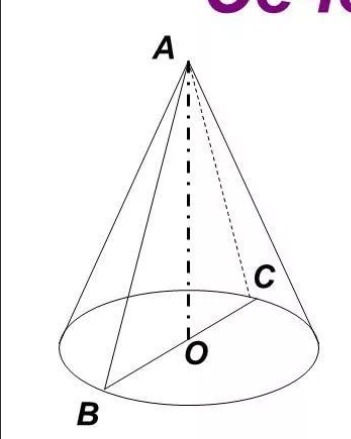
Осевое сечение конуса это р/б треугольник, диаметр основания - основание треугольника, образующие, выходящие из концов данного диаметра , боковые стороны.
Этот треугольник также прямоугольный , углы при основании равны, а сумма острых углов в прямоугольном треугольнике 90*. Найдём их градусные меры
∠АВС=∠АСВ=90/2=45*
Площадь прямогугольника с равными катетами
ВА- образующая
Проведем высоту к основанию(АО) , она разделит р/б треугольник на два равных прямоугольных треугольника, также она будет являтся биссектрисой.
∠ВАО=∠ОАС=45*=∠В=∠С
ΔАОВ- прямоугольный и р/б(BO=AO, ВА-гипотенуза)
По теореме Пифагора:
BO,AO-x
х=5см=ВО - радиус основания
В основании цилиндра лежит окружность,её площадь:
S=5^2pi=> 25pi " alt=" S=pi*r^2 ->S=5^2pi=> 25pi " align="absmiddle" class="latex-formula">
