|3x-4|+|5x-6|<2 Решал с помощью общего метода решения неравенств с модулем и получился...

Question

Дан 1 ответ

alkorb_zn · Answer 1 · 2018-09-11T01:48:01+0000

найдем корни уравнения: |3x-4|+|5x-6|=2

Для этого рассмотрим 3 случая

Сначала найдем нули подмодульных выражений:

$1) \ 3x-4=0 \\ \\ x=\frac{4}{3} \\ \\ 2) \ 5x-6=0 \\ \\ x=\frac{6}{5}$

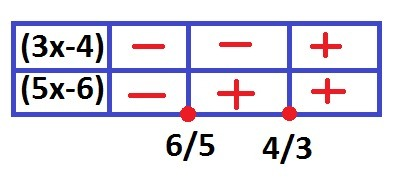
знаки, с которыми раскроется модуль удобно представить в таблице (см. рисунок)

1 случай)

$\left\{\begin{matrix}x<\frac{6}{5} \\ \\ -(3x-4)-(5x-6)=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x<\frac{6}{5} \\ \\ -3x+4-5x+6=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x<\frac{6}{5} \\ \\ 8x=8\end{matrix}\right. \Leftrightarrow \\ \\ \\ \Leftrightarrow \left\{\begin{matrix}x<\frac{6}{5} \\ \\ x=1 \end{matrix}\right. \Leftrightarrow x=1$

2 случай)

$\left\{\begin{matrix}\frac{6}{5}\leq x \leq\frac{4}{3} \\ \\ -(3x-4)+(5x-6)=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \frac{6}{5}\leq x \leq \frac{4}{3}\\ \\ -3x+4+5x-6=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \frac{6}{5}\leq x \leq\frac{4}{3} \\ \\ 2x=4\end{matrix}\right. \\ \\ \\ \Leftrightarrow \left\{\begin{matrix} \frac{6}{5}\leq x \leq\frac{4}{3} \\ \\ x=2 \end{matrix}\right. \Leftrightarrow x \in \ \varnothing$

3 случай)

\frac{4}{3} \\ \\ (3x-4)+(5x-6)=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ 3x-4+5x-6=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ 8x=12\end{matrix}\right. \Leftrightarrow \\ \\ \\ \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ x=\frac{3}{2} \end{matrix}\right. \Leftrightarrow x=\frac{3}{2} " alt=" \left\{\begin{matrix}x > \frac{4}{3} \\ \\ (3x-4)+(5x-6)=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ 3x-4+5x-6=2\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ 8x=12\end{matrix}\right. \Leftrightarrow \\ \\ \\ \Leftrightarrow \left\{\begin{matrix} x > \frac{4}{3} \\ \\ x=\frac{3}{2} \end{matrix}\right. \Leftrightarrow x=\frac{3}{2} " align="absmiddle" class="latex-formula">

в итоге из 3-х случаев получаем 2 корня: 1 и 3/2

Наносим их на координатную прямую (метод интервалов):

|3x-4|+|5x-6|<2</p>

|3x-4|+|5x-6|-2<0</p>

+++(1)---(3/2)+++>x

$OTBET: \ x \in (1; \ \frac{3}{2} )$