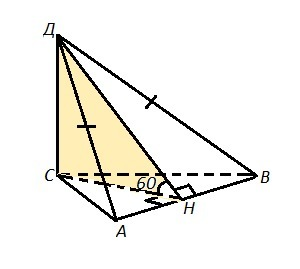
ΔАВС - равносторонний , АВ=АС=ВС=а .
Угол между пл. АВД и пл. АВС = 60°. Этот угол образован перпендикуляром ДН в плоскости АВД и высотой СН треугольника АВС. Точка Н - середина стороны АВ. ДН ⊥АВ, т.к. ΔАВС - равнобедренный (АД=ВД как наклонные, у которых равные проекции АС и ВС).
СН=а√3/2 ( высота равностороннего треугольника)
ΔСДН: ∠ДСН=90° , т.к. по условию ДС⊥ пл. АВС ⇒ ДС⊥любой прямой в пл. АВС.
∠ДНС=60°, ДС/СН=tg60° ⇒ ДC=CН*tg60°=(а√3/2)*√3=3а/2
S(АВС)=а²√3/4 (площадь равностороннего треугольника)
V(пир.)=1/3*h*S(осн.)=1/3*ДС*S(АВС)=1/3*3а/2*(а²√3/4)=а³√3/8 .