Нам даны три вершины вписанного четырехугольника: А, В и С. Надо найти четвертую вершину, удовлетворяющую условию задачи.
Свойства: У вписанного четырехугольника сумма протволежащих углов равна 180°. МAB+
Центр вписанной в четырехугольник окружности лежит на пересечении биссектрис его углов. (2)
Определение условий для построения
Пусть центр вписанной окружности О, тогда в четырехугольнике АВСО:
<АОС = 360° - <ВАО-<АВС-<ВСО или </p>
<АОС = 360° - <АВС - ((1/2)*<МАВ + (1/2)<МСB)) (из 2). </p>
Но из (1) ясно, что (1/2)*<МАВ + (1/2)*<МСB =90°. </p>
Значит для удовлетворения условий задачи необходимо, чтобы
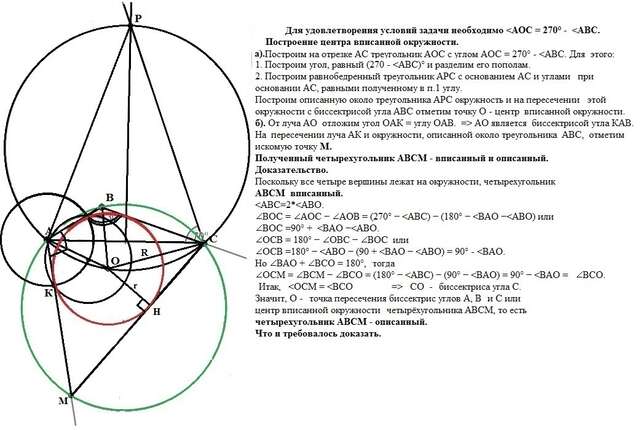
<АОС = 270° - <АВС.</p>
а). Построение центра вписанной окружности.
Построим на отрезке АС треугольник АОС с углом
АОС = 270° - <АВС. Для этого: </p>
1. Построим угол, равный (270 - <АВС)° и разделим его пополам. </p>
2. Построим равнобедренный треугольник АРС с основанием АС и углами при основании АС, равными полученному в п.1 углу.
Построим описанную около треугольника АРС окружность и на пересечении этой окружности с биссектрисой угла АВС отметим точку О - центр вписанной окружности.
б). Найдем точку М: От луча АО отложим угол ОАК = углу ОАВ. => АО является биссектрисой утла КАВ. На пересечении луча АК и окружности, описанной около треугольника АВС, отметим искомую точку М.
Полученный четырехугольник АВСМ - вписанный и описанный.
Доказательство.
Поскольку все четыре вершины лежат на окружности, четырехугольник АВСМ вписанный.
∠BОC = ∠AОC − ∠AОB = (270° −
∠BОC =90° +
∠OCB = 180° − ∠OBC − ∠BOC или
∠OCB =180° −
Но ∠BAO + ∠BCO = 180°, тогда
∠OCМ = ∠BCМ − ∠BCO = (180° −
Итак, CO - биссектриса угла C.
Значит, О - точка пересечения биссектрис углов A, B и C или центр вписанной окружности четырёхугольника ABCМ, то есть четырехугольник АВСМ - описанный.
Что и требовалось доказать.
P.S. Порядок построения углов, равных данному и углов, равных половине данного, нахождение центра вписанной и описанной окружности, так же как и построение серединного перпендикуляра к отрезку и перпендикуляра из точки к прямой опущен, так как это стандартные построения.
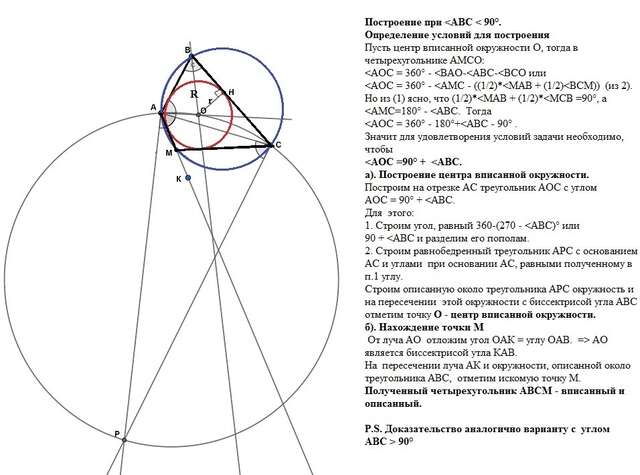
Если угол АВС<90, то построение аналогично, за исключением того, что равнобедренный треугольник строится на основании АС с углами при основании равными (360-(270-<ABC))/2 = 90°+<ABC. В полуплоскости (относительно прямой АС), не содержащей точку В (смотри второе приложение).</p>