Дано:
H = 8 см = 0,08 м
g = 10 м/с²
ρ(с) = 400 кг/м³
ρ(в) = 1000 кг/м³
================
Найти: h - ?
================
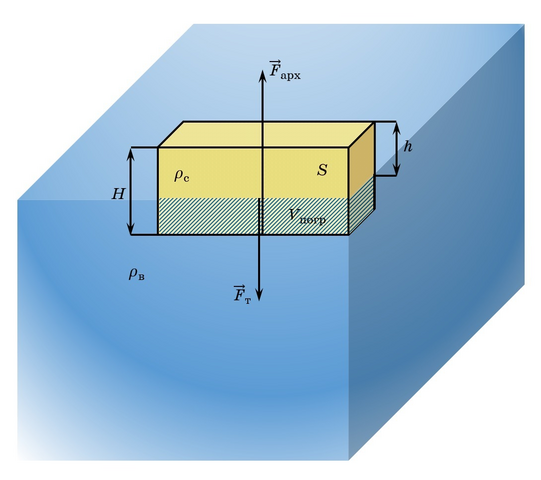
Решение. На доску плавающую на поверхности воды действует две силы: сила тяжести (Fт) и сила Архимеда (Fарх), которые уравновешивают друг друга (см. рисунок).
Из условия плавания тел: Fарх - Fт = 0 ⇒ Fарх = Fт
Fт = m(с)g; m = ρ(с)V(с); V = SH ⇒ Fт = ρ(с)SHg
Fарх = ρ(в)gV(погр); V(погр) = (H - h)S ⇒ Fарх = ρ(в)g(H - h)S
Следовательно, ρ(с)SH = ρ(в)g(H - h)S
ρ(с)H = ρ(в)(H - h)
ρ(с)H = ρ(в)H - ρ(в)h
ρ(в)H - ρ(с)H = ρ(в)h
H(ρ(в) - ρ(с)) = ρ(в)h
h = H(ρ(в) - ρ(с))/ρ(в)
Определим значение искомой величины:
[h] = м · (кг/м³ - кг/м³)/кг/м³ = м · кг/м³/кг/м³ = м
h = 0,08 · (1000 - 400)/1000 = 0,048 м = 4,8 см
Ответ: h = 4,8 см.