Срочноооо 21 задание

Question

Срочноооо 21 задание

---

Answer 1

иррациональные неравенства делятся на два типа:

и

g(x) " alt=" \sqrt{f(x)} > g(x) " align="absmiddle" class="latex-formula">

в нашем (первом) случае решением будет система:

{ f(x) >= 0

{ g(x) > 0

{ f(x) < (g(x))²

я немного прокомментировала неравенства из этой системы...

Answer 2

√(x² + 3x + 2) ≤ -x + 1; √(x² + 3x + 2) + x - 1 ≤ 0; Используем метод интервалов.

1) у = √(x² + 3x + 2) + x - 1; x² + 3x + 2 ≥ 0; x₁ = -2; x₂ = -1; D(y) = (-∞; -2]∪[-1; ∞);

2) y = 0; √(x² + 3x + 2) + x - 1 = 0; √(x² + 3x + 2) = -x + 1; x² + 3x + 2 = (-x + 1)²; x² + 3x + 2 = x² + 1 - 2x; 5x = -1; x = -0,2.

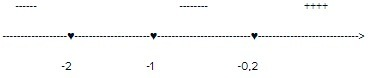
3) координатная прямая во вложении

Ответ: (-∞; -2]∪[-1; -0,2].

---

Comments

это не метод интервалов (здесь на множители не разложить...) и неравенство строгое, потому -0.2 не является решением...

---

Это метод интервалов, который называется "обобщённый метод интервалов"