Камень брошен под некторым углом к горизонту. Он достиг максимальной высоты 20м. Его...

Question 1

Камень брошен под некторым углом к горизонту. Он достиг максимальной высоты 20м. Его скорость на этой высоте равна 15м/c. Под каким углом к горизонту камень упадет на землю?

Question 2

легко сказать ничего не понять спасибо помог.

Question 3

(нет)

Question 4

Ответ arctg(4/3)

Question 5

а можно решение?

Question 6

Есть такая формула: h_max = υ₀×sin²α/2g, где υ₀ = υₓ/cosα, значит, h_max = υₓ²×tg²α/2g ⇒ tgα = √(h_max×2g/υₓ²) = √(20×2×10/225) = 4/3Следовательно, α = arctg(4/3)

Question 7

Понятно?

Question 8

У меня тоже сейчас каникулы, но я каждый день что-то для себя решаю (для подготовки к ВНО) и по возможности помогаю другим.

Question 9

Дано:

$h_{max} = 20$ м

$v_{0x} = 15$ м/с

$g = 10$ м/с²

=======================

Найти: α - ?

=======================

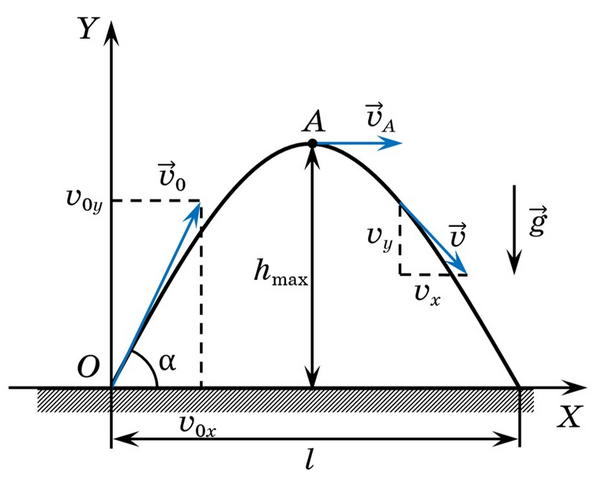
Решение. Если сопротивление воздуха не учитывать, то высота подъёма камня: $h_{max} = \frac{v_{0}^{2}sin^{2}\alpha}{2g}$ . В выбранной системе координат, начальная скорость ( $v_{0}$ ) направлена под углом (α) к горизонту: $v_{0x} = v_{0}cos\alpha$ ⇒ $v_{0} = \frac{v_{0x}}{cos\alpha}$

Значит высота подъёма камня равна $h_{max} = \frac{(\frac{v_{0x}}{cos\alpha})^{2}sin^{2}\alpha}{2g} = \frac{v_{0x}^{2}sin^{2}\alpha}{2gcos^{2}\alpha} = \frac{v_{0x}^{2}}{2g} * tg^{2}\alpha$ . Отсюда $tg\alpha = \sqrt{\frac{h_{max}*2g}{v_{0x}^{2}}}$

Определим значение искомой величины:

$tg\alpha = \sqrt{\frac{20*2*10}{15^{2}} } = \sqrt{\frac{400}{225}} = \frac{20}{15} = \frac{4}{3}$ ⇒ $\alpha = arctg\frac{4}{3}$

Ответ: $\alpha = arctg\frac{4}{3}$

Question 10

Можете пожалуйста пмочь с https://znanija.com/task/29355461 ?

Question 11

Главное, что ответ правильный.

Question 12

Нет, я не знаю этого человека. Просто везение в никах)

Question 13

Так уж и быть. Выкладываю своё простое решение.

Question 14

Можете пожалуйста пмочь с https://znanija.com/task/29355461 ?