Площадь боковой поверхности правильной четырёхугольной пирамиды равна 240см², сторона...

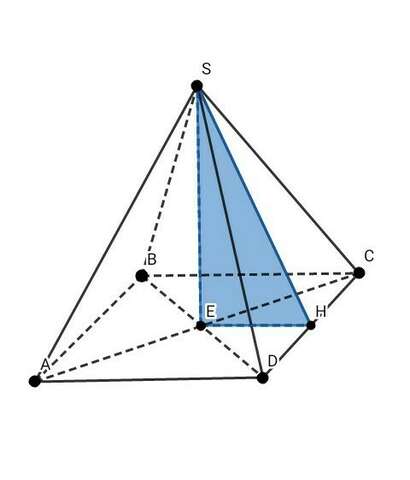
ДАНО: АВСDS - правильная четырёхугольная пирамида ; S бок. = 240 см² ; ABCD - квадрат ; АВ = 12 см.

НАЙТИ: V ( пирамиды )
___________________________

РЕШЕНИЕ:

1) В правильной четырёхугольной пирамиде боковые грани равны =>

S бок. = 240 см²

4 × S cds = 240 см²

S cds = 60 см²

Проведем в боковой грани пирамиды высоту SH ( апофема ), ∆ CDS — равнобедренный ( боковые рёбра пирамиды равны )

S cds =1/2 × СD × SH

60 = 1/2 × 12 × SH

SH = 10 см

2) Так как пирамида правильная, значит, вершина пирамиды проецируется в центр его основания ( квадрата ). Центром квадрата является точка пересечения его диагоналей.

SE перпендикулярен ЕН
SH перпендикулярен CD

Значит, по теореме о трёх перпендикулярах
ЕН перпендикулярен CD

EH = 1/2 × AD = 1/2 × 12 = 6 см

3) Рассмотрим ∆ SHE ( угол SEH = 90° ):

По теореме Пифагора:

SH² = SE² + EH²

SE² = 10² - 6² = 100 - 36 = 64

SE = 8 см

4) V ( пирамиды ) = 1/2 × S осн. × h = 1/2 × S abcd × SE =

$= \frac{1}{3} \times 12 \times 12 \times 8 = 4 \times 12 \times 8 = 384 \\$

ОТВЕТ: V ( пирамиды ) = 384 см³