С высокой башни одновременно брошены два тела с одинаковыми по модулю начальными...

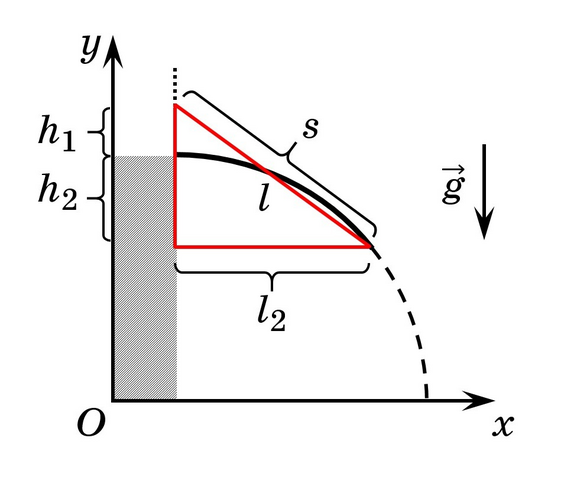
Пусть 1 - это тело, брошенное вертикально вверх; 2 - тело, брошенное горизонтально. Тогда...

Дано:

$v_{0x1} = 0$ м/с

$v_{0y1} = 8$ м/с

$v_{0x2} = 8$ м/с

$v_{0y2} = 0$ м/с

$t = 1$ с

$g = 10$ м/с²

===================

Найти: $s - ?$

===================

Решение. Тело 2 имеет прямолинейное движение по оси $Ox$ , поэтому его расстояние по оси $Ox$ равно:

$l_{2} = v_{0x2}t = 8 \cdotp 1 = 8$ м,

а по оси $Oy$ тело движется равноускоренно, поэтому его расстояние по оси $Oy$ равно:

$h_{2} = \frac{gt^{2}}{2} = \frac{10 \cdotp 1^{2}}{2} = 5$ м

Тело 1 двигалось только по оси $Oy$ и расстояние, которое оно прошло равно:

$h_{1} = v_{0y1}t - \frac{gt^{2}}{2} = 8 \cdotp 1 - \frac{10\cdotp 1^{2}}{2} = 3$ м.

Значит, общая высота между этими телами через 1 секунду равно:

$h = h_{1} + h_{2} = 3 + 5 = 8$ м.

Получается прямоугольный треугольник (см. рисунок). Определим по теореме Пифагора гипотенузу s:

$s = \sqrt{h^{2} + l_{2}^{2}} = \sqrt{8^{2} + 8^{2}} = 8\sqrt{2} \thickapprox 11,3$ м.

Ответ: $s \thickapprox 11,3$ м.