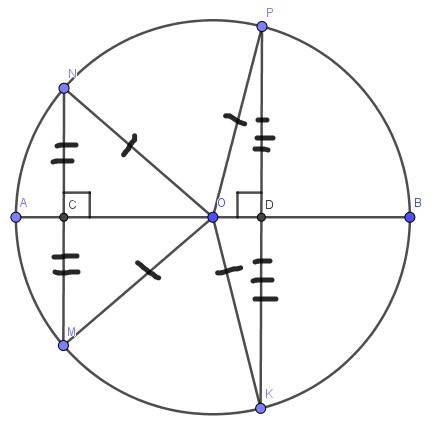
Пусть О - центр окружности.
Проведем радиусы ON=OM=OK=OP=R
по условию: NC=CM и PD=DK ⇒ ОА и OB - медианы
ΔOPK и ΔMON- равнобедренные, значит ОА и OB - также и высоты
∠NCO+∠PBO=90°+90°=180°
Для прямых NM, PK и секущей AB сумма внутренних односторонних углов равна 180° ⇒ MN || PK - ч.т.д