Вопрос в картинках...

$\frac{2 }{x } =\frac{\sqrt{5-4x }}{x^{2}} +\frac{1 }{5-4x }$

\frac{(5 - {y}^{2} )}{4} = x" alt="{\sqrt{5-4x }} = y \: \: \: = > \frac{(5 - {y}^{2} )}{4} = x" align="absmiddle" class="latex-formula">
$\frac{8}{5 - {y}^{2} } = \frac{16 {y} }{(5 - {y}^{2}) ^{2} } + \frac{1}{ {y}^{2} }$
$\frac{8}{5 - {y}^{2} } - \frac{16 {y} }{(5 - {y}^{2}) ^{2} } = \frac{1}{ {y}^{2} }$
$\frac{8(5 - {y}^{2}) - 16y }{ {(5 - y ^{2} )}^{2} } = \frac{1}{ {y}^{2} }$
$\frac{8(5 - {y}^{2} - 2y)}{(5 - {y}^{2}) ^{2} } = \frac{1}{ {y}^{2} }$
8y²(5-y²-2y)=25+y⁴-10y²
25+y⁴-10y²-8y²(5-y²-2y)=0
y⁴-10y²+25+8y²(y²+2y-5)=0
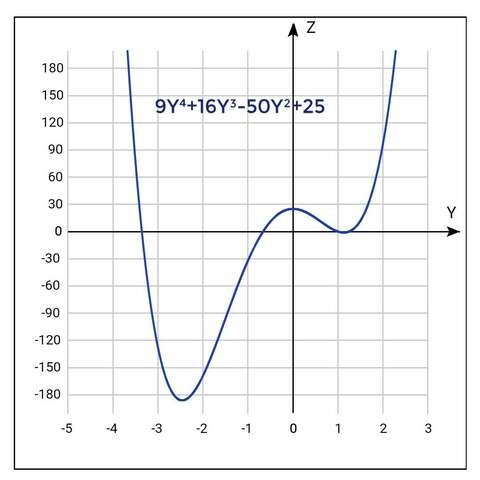
9y⁴+16y³-50y²+25=0
у=1 является корнем, действительно,
подставим его в наше уравнение
9*1⁴+16*1³-50*1²+25=0

разделим (9y⁴+16y³-50y²+25) на (x-1)
столбиком (см рис, только там у меня u, а не у, но, думаю, суть та же)
(y-1)(9y³+25y²-25y+25)=0
у1=1

9y³+25y²-25y+25=0
решаем по методу Виета-Кардано (см рис)
решения приблизительные
отрицательные нам не подходят,
( у=✓(5-4х)>0
поэтому
остаётся лишь

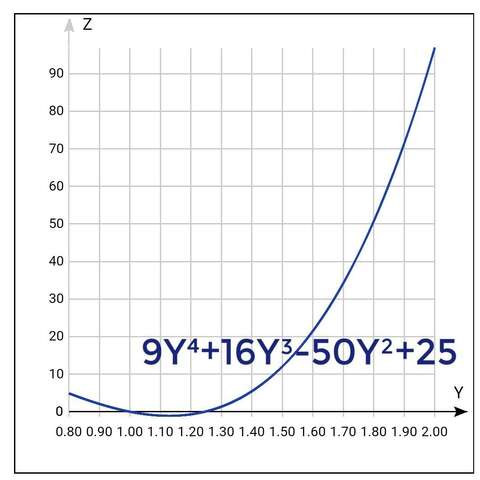
у2≈1,245

вернёмся к замене
✓(5-4x)=1
5-4x=1
x1=1

✓(5-4x)≈1,245
5-4x≈1,55
x2≈0,86

ОДЗ уравнения 5-4х>0(х<5/4), х≠0<br>оба корня подходят

Ответ
x1=1
x2≈0,86

удачи!