Боковые ребра прямоугольного параллелепипеда равны и перпендикулярны основанию, поэтому перпендикулярны любой прямой в его плоскости.=> DD1⊥DH, DD1=AA1=2√3.
Расстояние от точки до прямой равно длине перпендикуляра, проведенного из данной точки к данной прямой. Искомое расстояние – длина перпендикуляра D1H. Треугольник DD1Н прямоугольный. По т.Пифагора D1H=√(DD1²+DH²)
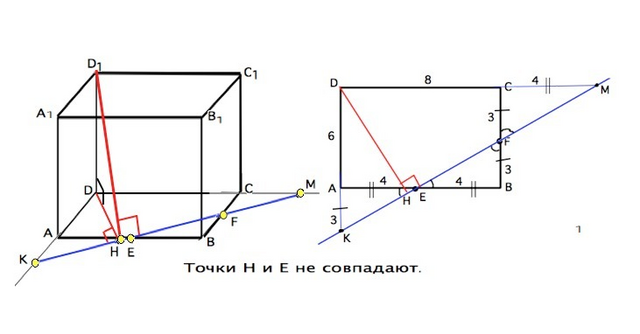
По условию АЕ=ВЕ=8:2=4, CF=BF=6:2=3 Продлим ЕF в обе стороны до пересечения с продолжениями DА и DС в точках К и М соответственно. Прямоугольные ∆ АКЕ =∆ ВЕF равны по катету (АЕ=ВЕ) и острому углу при Е ( вертикальные). Аналогично ∆ ВЕF=∆ EMF (CF=DF, вертикальные острые углы при D равны). Следовательно, АК=FB=3, СМ=ВЕ=4, и в ∆ KDM катеты DK=AD+AK=9, DM=DC+CM=12.
DН пп ЕF, => по т. о 3-х перпендикулярах DH пп EF и является высотой прямоугольного треугольника KDM.
Из площади прямоугольного треугольника S=KD•DM:2=DH•KM:2 следует DH=KD•MD:KM
По т.Пифагора КМ=√(KD²+DM²)=√(9²+12²)=15
DH=√(9•12:15)=7,2
D₁H=√[(2√3)*+(7,2)*]=√(6384/100)=(4√399):10=