Катеты прямоугольного треугольника равны 3 и 4. окружность, проходящая через середины...

Question

Катеты прямоугольного треугольника равны 3 и 4. окружность, проходящая через середины гипотенузы и меньшего катета, касается другого катета. Найдите длину хорды этой окружности, высекаемой на гипотенузе

Answer 1

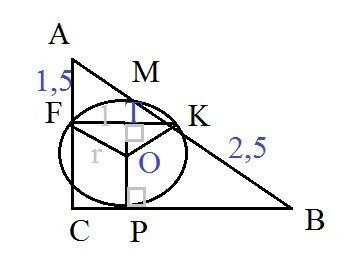
F- середина катета АС; АС=3

K- cередина гипотенузы АВ; АВ=5;

FK - средняя линия Δ АВС; FK=2

Р - точка касания окружности и катета ВС.

Радиус ОР ⊥ ВС.

Диаметр ОР ⊥ FK (FK||BC) и делит хорду FK пополам.

FT=TK=1

CP=FT=TK=1

BP=3

Применяем свойство

Произведение секущей на ее внешнюю часть равно квадрату касательной:

BM·BK=BP

(2,5+MK)·2,5=3²

2,5MK=9-6,25

MK=1,1

О т в е т. 1,1

---