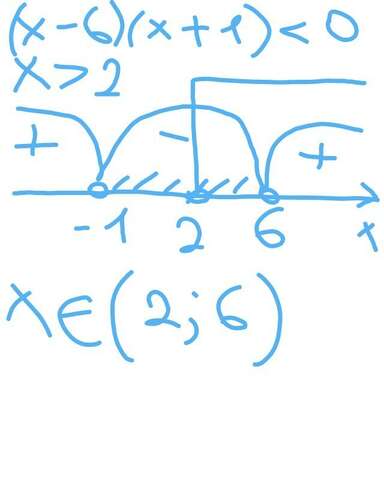x - 2 \\ x + 10 > {x}^{2} - 4x + 4 \\ {x}^{2} - 5x - 6 < 0 \\ d = {b}^{2} - 4ac = 25 - 4 \times ( - 6) = 25 + 24 = 49 \\ x1 = \frac{5 + 7}{2} = \frac{12}{2} = 6 \\ x2 = \frac{5 - 7}{2} = \frac{ - 2}{2} = - 1 \\ (x - 6)(x + 1) < 0" alt=" log_{3}(x - 2) < log_{9}(x + 10) \\ log_{3}(x - 2) < log_{ {3}^{2} }(x + 10) \\ log_{3}(x - 2) < \frac{1}{2} log_{3}(x + 10) \\ log_{3}(x - 2) < log_{3} {(x + 10)}^{ \frac{1}{2} } \\ log_{3}(x - 2) < log_{3} \sqrt{x + 10} \\ x- 2 < \sqrt{x + 10} \\ \sqrt{x + 10} > x - 2 \\ x + 10 > {x}^{2} - 4x + 4 \\ {x}^{2} - 5x - 6 < 0 \\ d = {b}^{2} - 4ac = 25 - 4 \times ( - 6) = 25 + 24 = 49 \\ x1 = \frac{5 + 7}{2} = \frac{12}{2} = 6 \\ x2 = \frac{5 - 7}{2} = \frac{ - 2}{2} = - 1 \\ (x - 6)(x + 1) < 0" align="absmiddle" class="latex-formula">
ОДЗ:

0 \\ x > 2 \\ \\ x + 10 > 0 \\ x > - 10" alt="x - 2 > 0 \\ x > 2 \\ \\ x + 10 > 0 \\ x > - 10" align="absmiddle" class="latex-formula">
=> х > 2.
Далее во вложении.
Наибольшее целое решение -- 5.
Ответ: 5.