Все вектора выделены жирным.
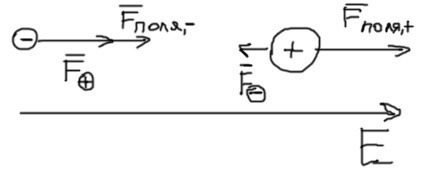
Для начала нужно разобраться какие силы действуют в задачи. Каждая частица движется, скажем, "вперёд", под действием внешнего поля с напряжённость в E.
Так же заряды притягиваются друг к другу, на отрицательно заряженную частицу действует сила её притяжения к "плюсу" — F₊.
На положительно заряженную частицу действует сила притяжения к "минусу" — F₋, которая направлена противоположно к силе действующей со стороны внешнего электрического поля.
*смотрим на картинку*
При решении таких задач, нужно определить первоначальное, "балансное" уравнение, которое может заключатся в каких-то подсказках, законах сохранения чего-там либо... В данном случае, мы знаем, что с течением времени расстояние между частицами не изменяется. В условиях данной задачи, это значит что обе частицы движутся с одинаковым ускорением:
а₋ = а₊
Тогда, согласно второму закону Ньютона:
F-,рез/m = F+,рез/M
Где, Fрез — результирующая сила действующая на каждую из частиц. Она равна векторной сумме действующих на неё сил.
Выразим эту силу для каждой частицы и избавимся от вектора. Будем использовать схемку в качестве напоминашки о направлении действия сил:
F₋, рез = F₊ + Fполя,₋
F₊, рез = Fполя,₊ — F₋
Сила которое поле оказывает на частицу F=E*q. Соответственно для каждой частицы: Fполя₋ = E*q; Fполя₊ = E*Q
Cила воздействия между частицами берётся из закона Кулона. Именно тут фигурирует нужное нам расстояние между частицами:

Где k — табличный коэф. среды; q1,q2 — заряды; r — искомое расстояние между частицами.
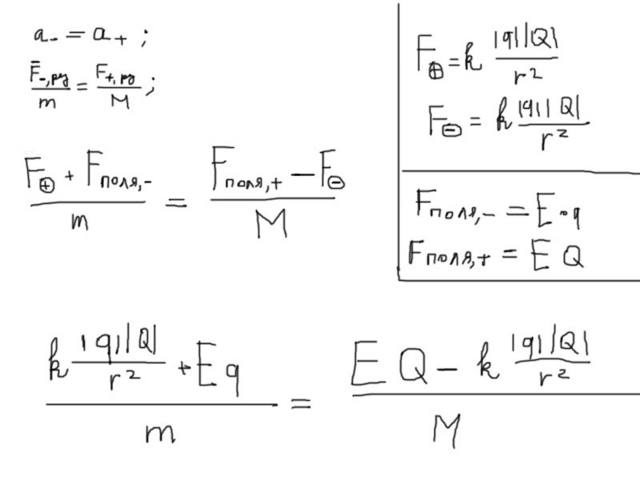
Вставим это всё в одно уравнение, и получим уравнение только с одним неизвестным — нужным для нас расстоянием r.
Подставим это всё, обратно, в формулу и получим монстра, выразив из которого "r" мы решим задачу. На этом этапе я только оставлю свой рисунок с подставленными значениями.
После того как мы выразим и высчитаем "r", мы сможем его подставить обратно, в любую из частей уравнения и получим значение акселлерации. Они у обоих частиц одинаковы. Удачи с выражением^^