√(2x - 1) + √(x + 15) ≤ 5; √(2x - 1) + √(x + 15) - 5 ≤ 0;
Нерівність розв'яжемо за допомогою узагальненого методу інтервалів.
1) y = √(2x - 1) + √(x + 15) - 5; x ≥ 0,5 i x ≥ -15. D(y) = [0,5; ∞)
2) y = 0; √(2x - 1) + √(x + 15) - 5 = 0; √(2x - 1) = -√(x + 15) + 5;
2x - 1 = x + 15 + 25 - 10√(x + 15); 10√(x + 15) = 41 - x; 100(x + 15) = (41 - x)²;
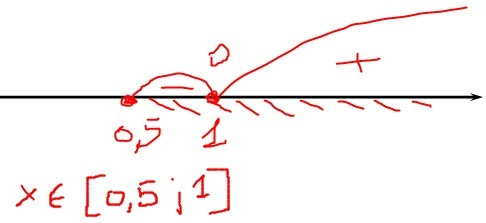
100x + 1500 = 1681 + x² - 82x; x² - 182x + 181 = 0; x₁ = 1; x₂ = 181 - не задовольняє рівняння √(2x - 1) + √(x + 15) - 5 = 0 (тому не є нулем функції).