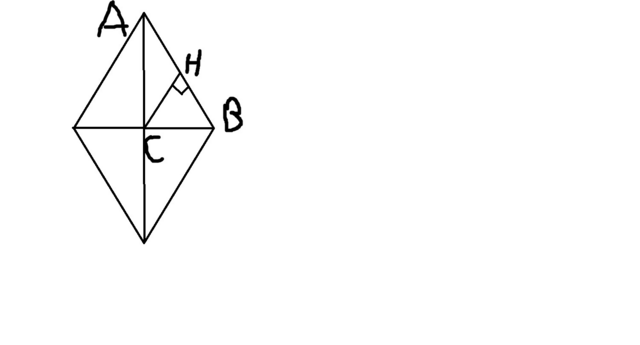
Перпендикуляр - является высотой в прямоугольном треугольнике ABC.
У нас есть высота и длины отрезков, на которые поделена сторона. Сразу вспоминаются метрические соотношения. Есть 4 формулы по метрическим соотношениям:
1) h = ab÷c , где a,b - катеты. c - гипотенуза
2) h² = uv , где u, v - отрезки, на которые поделена гипотенуза.
3) a² = vc, где v - отрезок на который поделена гипотенуза, а c - гипотенуза.
4 ) b² = uc, тоже самое что и в третьем, но другой отрезок
Нам подходит вторая формула:
144 = x(x-7)
x² - 7x - 144 = 0 ; По теореме Виета находим корни.
Корни:
1) 16
2) -9 сторонний корень. Потому что длина отрезка не может быть отрицательной.
Отсюда AH = 16, BH = 9
Теперь воспользуемся третьей формулой
AC² = 16*25 = 400
AC = 20;
По теореме Пифагора либо по четвертой формуле находим второй катет.
BC² = 9*25 = 225
BC = 15
Так как диагонали в ромбе делятся точкой пересечения пополам, то первая диагональ = 30 см. вторая = 40 см.