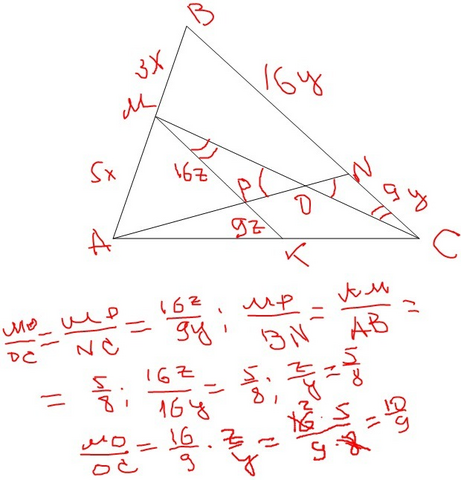
Проведемо МК || BC, тоді Трикутники МОР і NОС - подібні за двома кутами і трикутники АВС і АМК також подібні (згідно основної теореми подібності). З подібності трикутників, маємо: МО : ОС = МР : NC = (16z)/(9y); MP:BN = AM:AB = 5/8; 16z/16y = 5/8; z/y = 5/8.
Отже, МО/ОС = 16/9 · z/y = 16/9 · 5/8 = 10/9.
Відповідь: МО:ОС = 10:9