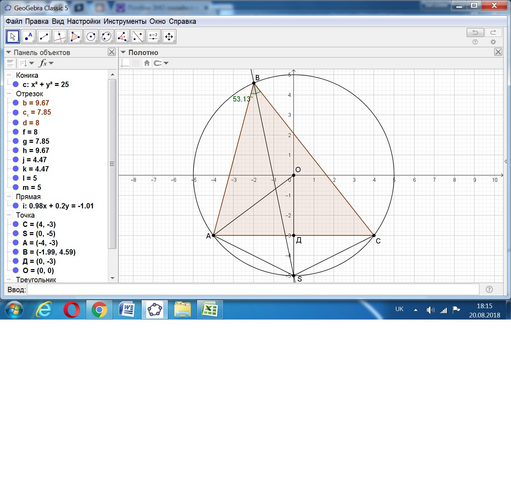
Хорды AS и SC равны ( стягивают равные дуги).
Тогда радиус ОS перпендикулярен АС.
По Пифагору SД = √((2√5)² - (8/2)²) = √(20 - 16) = √4 = 2.
Из треугольника АОД находим: R² = 4² + (R - 2)².
R² = 16 + R² - 4R + 4,
4R = 20,
R = 5.
Угол АОS = ∠В как центральный и 2 вписанных, опирающихся на одну дугу.
По теореме косинусов:
cos B = cos(AOS) = (R² + R² - (2√5)²)/(2*R*R) = (2*5² - 20)/2*5² = 30/50 = 3/5.
Угол В = arc cos(3/5) ≈ 0,927295218
радиан ≈ 53,13010235
°.