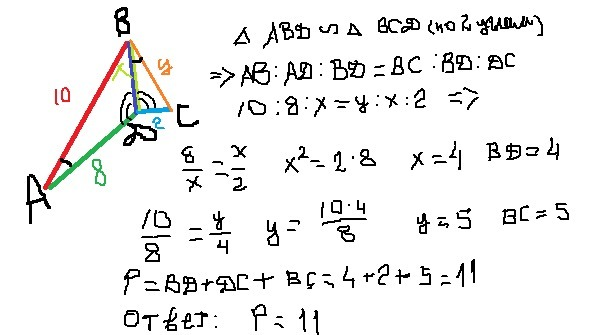Дано: ΔАВD и ΔBCD
BD - общая сторона.
∠BAD = ∠DBC
∠ADB = ∠BDC
AB = 10
AD = 8
DC = 2
Найти:P(BCD)
Решение.
Рассмотрим ΔАВD и ΔBCD. Два угла одного соответственно равны двум углам другого. (∠BAD = ∠DBC и ∠ADB = ∠BDC по условию) Следовательно, треугольники подобны,
Но мы не можем сказать, что они равны, так как не знаем про равенство сторон между этими углами.
Из подобия треугольников следует равенство отношений соответствующих сторон (т.е. лежащих против соответственно равных углов)
АD/BD = BD/DC; BD² = AD*DC; BD = √(AD*DC) = √(8*2) =√16 = 4
AB/BC = AD/BD; BC = (AB*BD)/AD = (10*4)/8 = 40/8 = 5
P(BCD) = BD + DC + BC = 4 + 2 + 5 = 11
Ответ:Р(ВСD) = 11