а) или
или 
Из 2-го уравнения следуют ограничения:  0; cosx>0 " alt=" sinx>0; cosx>0 " align="absmiddle" class="latex-formula">
0; cosx>0 " alt=" sinx>0; cosx>0 " align="absmiddle" class="latex-formula">
1-й корень отпадает, остаётся только:



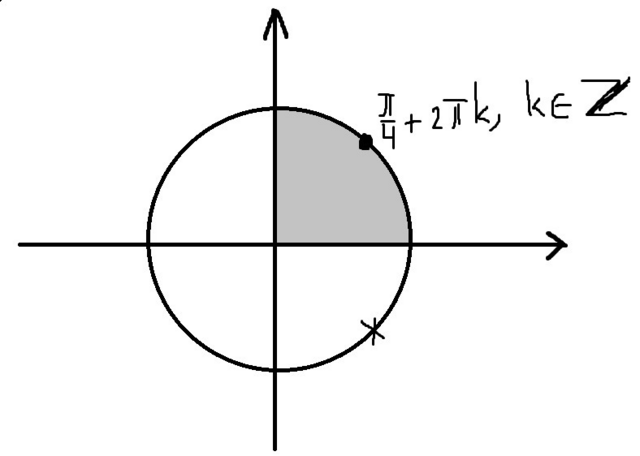
 , k - целое
, k - целое
б)

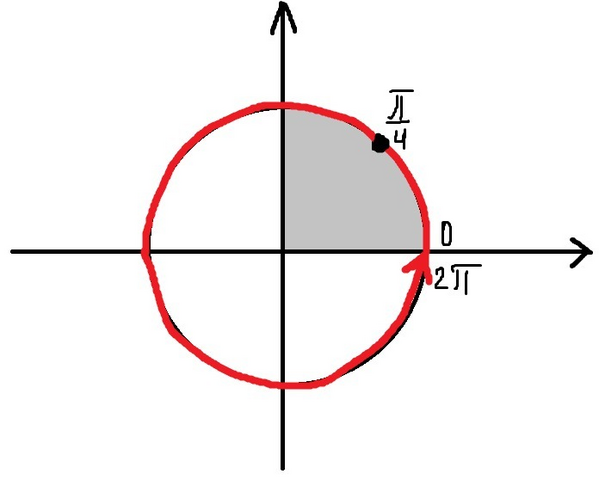
То есть промежуток ![(0; 2\pi ] (0; 2\pi ]](https://tex.z-dn.net/?f=+%280%3B+2%5Cpi+%5D+)
Отбор корней проведём с помощью тригонометрической окружности
Ответ: а)  k - целое; б)
k - целое; б) 
p.s. написал, потому что ничего не понял в прошлом решении