Напишу решение несколькими способами
1) Метод интервалов
x²-9>0
(x-3)(x+3)>0
___+___(-3)___-___(3)___+___
x∈(-∞; -3)U(3; +∞)
2) Разбитие на совокупность систем
x²-9>0
(x-3)(x+3)>0
Имеем произведение двух чисел, которое должно быть больше нуля. Так как "+" на "+" дает "+" и "-" на "-" дает "+"
0 \ \Leftrightarrow \ \left[\begin{array}{I} \left\{\begin{array}{I} x-3>0 \\ x+3>0 \end{array}} \\ \left\{\begin{array}{I} x-3<0 \\ x+3<0 \end{array}} \end{array}} \ \Leftrightarrow \ \left[\begin{array}{I}\left\{\begin{array}{I} x>3 \\ x>-3 \end{array}} \\ \left\{\begin{array}{I} x<3 \\ x<-3 \end{array}} \end{array}} \Leftrightarrow \ \left[\begin{array}{I} x>3 \\ x<-3 \end{array}} " alt=" (x-3)(x+3)>0 \ \Leftrightarrow \ \left[\begin{array}{I} \left\{\begin{array}{I} x-3>0 \\ x+3>0 \end{array}} \\ \left\{\begin{array}{I} x-3<0 \\ x+3<0 \end{array}} \end{array}} \ \Leftrightarrow \ \left[\begin{array}{I}\left\{\begin{array}{I} x>3 \\ x>-3 \end{array}} \\ \left\{\begin{array}{I} x<3 \\ x<-3 \end{array}} \end{array}} \Leftrightarrow \ \left[\begin{array}{I} x>3 \\ x<-3 \end{array}} " align="absmiddle" class="latex-formula">
x∈(-∞; -3)U(3; +∞)
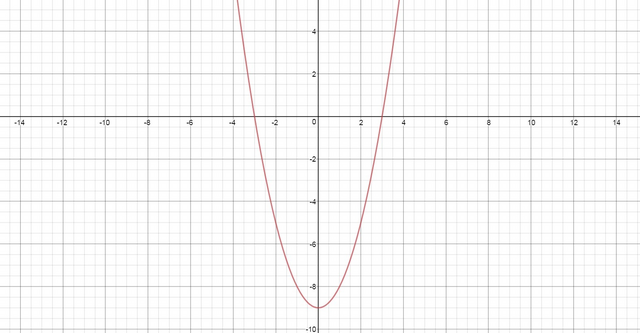
3) Графическое решение. Самое наглядное.
Строится парабола y=x²-9, после чего выбираются интервалы, где функция принимает значения больше нуля. График прикреплен.
x∈(-∞; -3)U(3; +∞)
