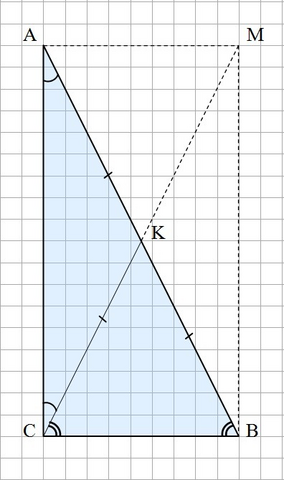
1). Строим произвольный прямоугольный треугольник АСВ. ∠АСВ = 90°.
В этом треугольнике - два острых угла: ∠САВ и ∠СВА.
Докажем, что сумма ∠САВ + ∠СВА = 90°.
2). Достраиваем треугольник АСВ до прямоугольника АМВС.
Диагонали прямоугольника равны и делятся точкой пересечения пополам. Тогда: АК = КВ = СК и СК - медиана ΔСАВ, проведенная к гипотенузе.
Образовались два равнобедренных треугольника: ΔАКС и ΔСКВ.
В ΔАКС: АК = СК => ∠КСА = ∠САК. (1)
В ΔСКВ: СК = КВ => ∠КСВ = ∠КВС. (2)
Так как в ΔАСВ прямой угол ∠АСВ = ∠КСА + ∠КСВ = 90°.
Учитывая (1) и (2), получим: ∠АСВ = ∠САК + ∠КВС = 90°.
Что и требовалось доказать.