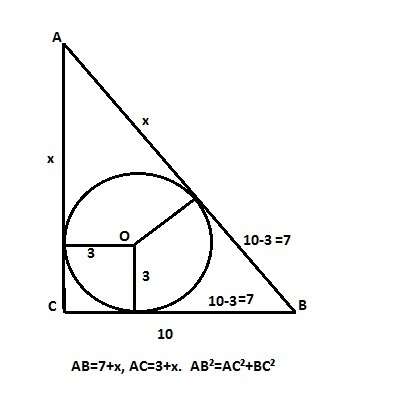
Радиус круга, описанного вокруг прямоугольного треугольника, равен половине его гипотенузы. Пусть треугольник АВС с прямым углом С. Пусть катет АС=10, тогда второй катет равен 3+х, а гипотенуза равна 7+х, так как отрезки от вершин до точек касания сторон с вписанной окружностью равны как касательные к окружности из одной точки. Тогда по Пифагору (7+х)²=10²+(3+х)². => 49+14x+x² =100+9+6x+x² => x=7,5. Следовательно, гипотенуза равна 14,5 см.
Тогда радиус описанной окружности равен 7,25 см.