99)
(х-у)²+(у-3)²=0
Т.к. квадраты (х-у)²≥0 и (у-3)²≥0, то равенство их суммы будет достигаться при равенстве каждого из слагаемых нулю
поэтому имеем х-у=0 и у-3=0
откуда х=3, у=3
100)
х²+у²+10х+12у+61=0
х²+10х+25+ у²+12у+36=0
(х+5)²+(у+6)²=0
аналогично рассуждая, получим равенство нулю каждого из слагаемых
откуда х+5=0 у+6=0
х= -5 у= -6
101)
|2х-4у-10|+|3х+у-1|=0
значение любого модуля всегда ≥0
поэтому равенство суммы двух модулей будет достигаться при равенстве каждого из этих модулей нулю.
а модуль будет равен нулю, когда подмодульное выражение равно нулю.
Получаем систему:
2х-4у-10=0
3х+у-1=0
или
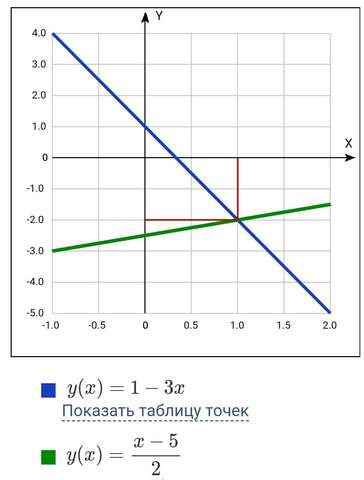
х-2у=5
3х+у=1
(решаем построением, см чертеж)
решением системы будут :
х=1
у= -2