1) Саша и Маша живут по одну сторону от дороги. Саша хочет пойти в гости к Маше, попутно...

Question

1) Саша и Маша живут по одну сторону от дороги. Саша хочет пойти в гости к Маше, попутно купив печенья в магазине у дороги. Где нужно построить магазин, чтобы расстояние, пройденное Сашей, было наименьшим? (Магазин можно строить только на дороге).

2) Саша и Таня живут по разные стороны от дороги, ограниченной двумя параллельными прямыми. Саша хочет пойти в гости к Тане (печенье она уже купила), но переходит дорогу Саша только по пешеходному переходу (перпендикулярно дороге). В каком месте нужно построить переход, чтобы расстояние, пройдённое Сашей, было наименьшим?

Answer 1

Наименьшее расстояние между двумя точками измеряется по прямой линии, соединяющей эти точки.

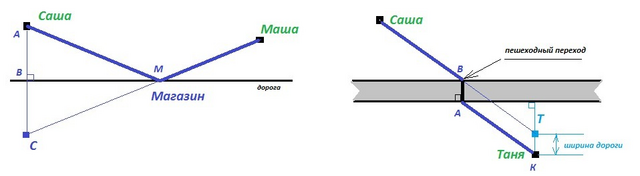
1) Саша и Маша живут по одну сторону дороги. Построим точку С, симметричную дому Саши относительно линии дороги : АВ=ВС; АВ⊥ВМ. Соединим точку С с домом Маши, а на пересечении с линией дороги поставим точку М.

В треугольнике АМС : МВ одновременно высота и медиана, значит, треугольник АМС - равнобедренный. АМ = СМ

Так как расстояние между домом Маши и точкой С наименьшее по построению, значит, путь Саши к дому Маши с посещением магазина в точке М будет самым коротким.

=========================================

2) Саша и Таня живут по разные стороны от дороги. Условно подвинем дом Тани в сторону дороги на расстояние ширины дороги и поставим точку Т. Соединим дом Саши и точку Т прямой линией и на пересечении с линией дороги со стороны Сашиного дома поставим точку В. Здесь и будет пешеходный переход ВА, перпендикулярный линии дороги.

Четырёхугольник ABTK : AB║TK - два перпендикуляра к линии дороги, АВ=ТК - ширина дороги. В четырёхугольнике АВТК две противоположные стороны равны и параллельны, значит, АВТК - параллелограмм, то есть АК=ВТ.

Так как расстояние между Сашиным домом и точкой Т было наименьшим по построению и АК=ВТ, следовательно, путь от Сашиного дома к Таниному по пешеходному переходу ВА будет самым коротким.

---