Раскроем модуль в первом уравнении и выделим полные квадраты.
1) (x² - 8x -16 + 32) + (y² + 8y - 8y) = 4 + 32.
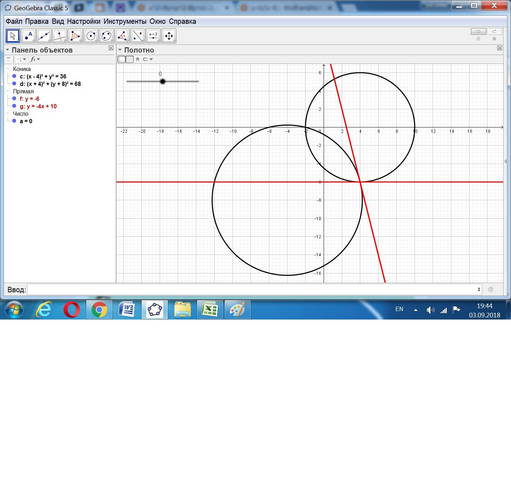
(x - 4)² + y² = 6² это окружность радиусом 6 с центром (4; 0).
2) (x² + 8x +16) + (y² + 8y + 8y + 64) = 4 + 64.
(x + 4)² + (y + 8)² = (√68)² это окружность радиусом √68 с центром (-4; -8).
Их общая часть - внешние участки окружностей между точками (-2; 0) и (4; -6).
Второе уравнение с параметром а - это прямая, поворачивающаяся вокруг точки (4; -6) при изменении параметра.
Система будет иметь 2 решения, когда прямая будет касательной к радиусам первой и второй окружностей.
Для меньшей окружности это а = 0, для большей - значение а как тангенс угла прямой к оси Ох равен (4 - (-4))/(-8 -(-6)) = 8/
(-2) = -4.
При изменении а в пределах от 0 до -4 прямая пересекает график в двух точках.
Ответ: а ∈ [-4; 0).