У Вас вообще-то написано не неравенство, а равенство
(x-2)(x+3)(x-1)/2=0
домножим обе части на 2≠0
(x-2)(x+3)(x-1)=0
так как , если произведение равно нулю , то это значит, что хотя бы один из множителей=0, поэтому
это уравнение распадается на три
(x-2)=0, откуда х¹=2
(x+3)=0, откуда х²=-3
(x-1)=0, откуда х³=1
если же надо решить , к примеру
(x-2)(x+3)(x-1)/2≥0, то поступаем так:
решаем уравнение, как описано выше , находим корни.
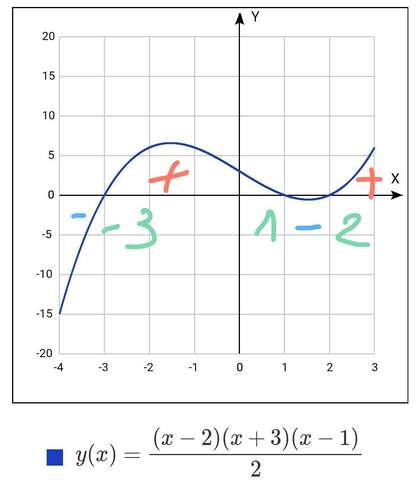
Это точки, в которых наша функция меняет знак
Найдем знак f(x)=(x-2)(x+3)(x-1)
на интервалах, на которые разбивают координатную ось корни уравнения:
(-∞,-3)
f(-5)=(-5-2)(-5+3)(-5-1)=-84<0<br>
(-3,1)
f(0)=(0-2)(0+3)(0-1)=6>0
(1,2)
f(1,5)=(1,5-2)(1,5+3)(1,5-1)=-1,125<0<br>
(2,+∞)
f(3)=(3-2)(3+3)(3-1)=18>0
Значит f(x)≥0
при х€ [-3,1]V[2, +∞)
а f(x)<0<br>при х€ (-∞,-3)V(1;2)
(см график)