Памогите плиз плочу 20 балов

Question

Памогите плиз плочу 20 балов

---

Comments

2 задачу тоже нереально решить ?

---

Если учесть, что CD (D я сам поставил) - это биссектриса (этому способствует и выделение одной дугой), то её решить можно.

---

можешь написать ка ?

---

Напишу, но я не отвечаю за правильно сделанного. Вдруг CD на самом деле не будет являться биссектрисой, но ладно. Решим хотя бы так.

---

правильность*

---

да ладно хот так

---

напишу

---

можешь прислать мне ответ ?

---

Сейчас решу, погоди.

---

ага спасибо зарание

Answer 1

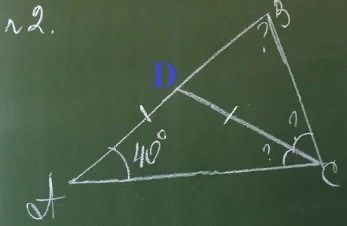
Дано: △ADC - равнобедренный (т.к. AD=DC)                                           ∠DAC=40° - по условию.                                                                                         CD - биссектриса.                                                                                                           Найти: ∠ACD, ∠BCD, ∠CBD.

Решение:                                                                                                                       1) △ADC - равнобедренный (т.к. AD=DC), значит ∠DAC=∠DCA=40°                            Сумма углов треугольника - 180°.                                                                             ∠ADC=180°-40°-40°=100°                                                                                            2)∠BDC и ∠ADC - смежные.                                                                                        ∠BDC=180°-∠ADC=180°-100°=80°                                                                             3)т.к. CD - биссектриса, то ∠ACD=∠DCB=40°                                                           Сумма углов треугольника - 180°.                                                                               ∠DBC=180°-∠BDC-∠BCD=180°-80°-40°=60                                                                  Ответ: ∠DBC=60°, ∠DCB=40°, ∠DCA=40°

---

Comments

Как-то так.

---

а откуда 40 крадусов