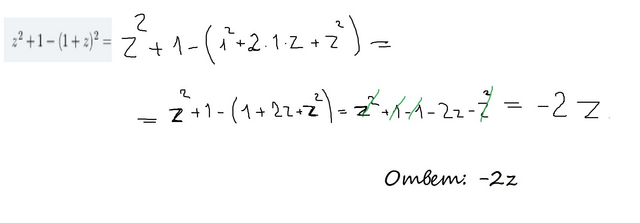Упростите выражение z²+1-(1+z)²

СЛУШАЙТЕ/ЧИТАЙТЕ ВНИМАТЕЛЬНО:

Сначала упростим (1+z)². Воспользуемся формулой сокращённого умножения "квадрат суммы" - (a+b)² = a²+2ab+b².

$\tt (1+z)^2 = 1^2+2\cdot1\cdot z+z^2 = 1+2z+z^2.$

Внимание! Перед скобкой стоит знак минус, а в скобах стоит целых два плюса. Как быть? Читаем следующее правило:

Если перед скобкам стоит знак минус, то при раскрытии скобок знаки ВСЕХ слагаемых в скобках меняются на ПРОТИВОПОЛОЖНЫЕ.

ПОЛУЧАЕМ:

$\tt z^2+1-(1+z)^2 \ = \ z^2+1-(1^2+2\cdot 1 \cdot z+z^2) \ = \ \\\\ \ = \ z^2+1-(1+2z+z^2) \ = \ z^2+1-1-2z-z^2 \ = \ -2z.$

ОТВЕТ: -2z

Пояснение: в последнем действии сокращаются z² и -z² (так как будет ноль), 1 и -1. Остаётся -2z.