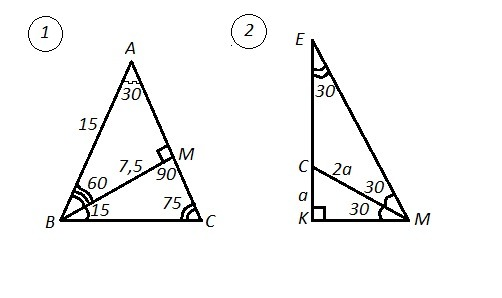
1) ΔАВС - равнобедренный, АВ=АС , ВМ⊥АС , ВМ=7,5 см, ∠МВС=15° .
ΔМВС: ∠ВМС=90°, ∠МСВ=90°-15°=75° ⇒ ∠АВС=∠АСВ (углы при оснрвании равнобедренного ΔАВС), ∠АВС=75° .
∠АВМ=∠АВС-∠МВС=75°-15°=60°
ΔАВМ: ∠АМВ=90° , ∠ВАМ=90°-∠АВМ=90°-60°=30° .
Против угла в 30° лежит катет ВМ, равный половине гипотенузы АВ ⇒
АВ=2·ВМ=2·7,5=15 (см) .
2) ΔМКЕ , ∠К=90° , ∠Е=30° , КЕ=12 см ,
МС - биссектриса ⇒ ∠СМЕ=∠СМК .
∠КМЕ=90°-∠Е=90°°-30°=60° ⇒ ∠СМЕ=∠СМК=60°:2=30° .
Обозначим отрезок КС через а: КС=а .
В ΔКМС катет КС лежит против угла в 30° ⇒ он равен половине гипотенузы СМ ⇒ СМ=2·КС=2а .
По теореме Пифагора: КМ²=СМ²-КС²=4а²-а²=3а² ⇒ КМ=а√3 .
Рассмотрим ΔМКЕ: ∠Е=30° ⇒ катет КМ лежит против этого угла, значит КМ равен половине гипотенузы МЕ ⇒ МЕ=2·КМ=2·а√3=2√3а .
По теореме Пифагора: МЕ²=КМ²+КЕ² , 4·3·а²=3а²+144 , 9а²=144 , а²=144/9 , а=12/3 .
МС=2а=24/3=8 (см) .
Смотри рисунки.