MN и PQ - параллельные прямые. Из точки А прямой MN проведена к PQ наклонная AB и...

Question

MN и PQ - параллельные прямые. Из точки А прямой MN проведена к PQ наклонная AB и перпендикуляр AC. Точка D расположена на MN,и прямая BD пересекает отрезок AC в точке E. Доказать, что ED = 2AB, то угол DBC = 1/3 угла ABC.

Answer 1

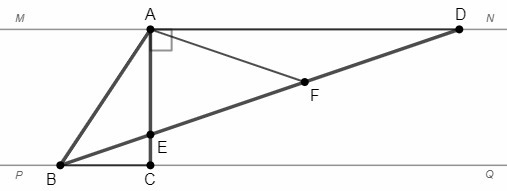
AC⊥PQ, MN||PQ => AC⊥MN

AF - медиана в △EAD

AF=ED/2 =AB (медиана из прямого угла равна половине гипотенузы)

△BAF - равнобедренный, ∠ABD=∠AFB

△AFD - равнобедренный, углы при AD равны

∠AFB=2∠ADB (внешний угол равен сумме внутренних, не смежных с ним)

∠ADB=∠DBC (накрест лежащие при MN||PQ)

∠ABD=∠AFB=2∠ADB=2∠DBC

∠ABC=∠ABD+∠DBC =3∠DBC <=> ∠DBC=∠ABC/3

---