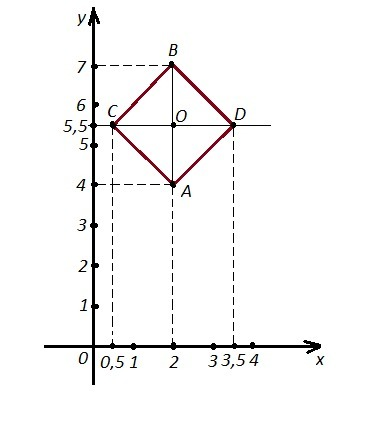
A(2;4) , B(2;7) ⇒ вершины диагонали АВ лежат на одной прямой х=2 .
Диагонали квадрата равны, перпендикулярны и в точке пересечения делятся пополам ⇒ длины диагоналей АВ и CD равны 7-4=3, половина длины АВ и CD = 3:2=1,5.
Вверх от точки А откладываем 1,5 , получаем точку О(2; 5,5) - середину диагоналей.
Проводим через точку О вторую диагональ CD перпендикулярно АВ и откладываем на ней вправо и влево от точки О отрезки длиной 1,5 .
Получаем оставшиеся вершины квадрата, точку С(0,5 ; 5,5) и точку D(3,5 ; 5,5) .