1)
f`(x)=2x^2-8
f`(x)=0 при 2x^2-8=0 при х=+/-2
участку 0 3 принадлежит х=2
находим f(x) при х = 0при х =2 и при х = 3
f(x)=0 при х = 0
при х =2 и при х = 3
f(x)=-10,6667
при х =2
f(x)=-6
при х =3
ответ min=f(2)=-10,(6)
max=f(0) = 0
2)
s`(t)=v(t)=12t-3t^2
v`(t)=12-6t
v``=-6
v`=0 при t=2 - точка абсолютного максимума
v(t=2)=12*2-3*2^2=12 - это ответ
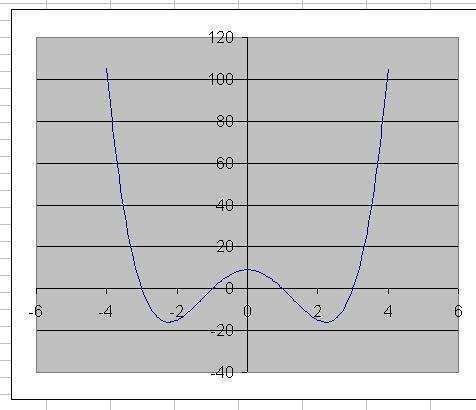
3) указанная функция четная, так как зависит от x^2
пусть t=x^2
y=t^2-10t+9
dy/dt=2t-10
экстремум (минимум) при t=5 (при х1=-корень(5) и x2= корень(5))
локальный максимум при t=0 (при x=0)
пересекает ось х при t=9 (при х3=-3 и x4= 3) и при t=1 (при х5=-1 и x6= 1)
точки перегиба искать лень
график прилагается
файл с построением графика в экселе прилагается
Скачать вложение Excel (XLS)