Два угла параллелограмма относятся как 5: 7. Найдите угол между высотами параллелограмма,...

Question

Два угла параллелограмма относятся как 5: 7. Найдите угол между высотами параллелограмма, проведенными с вершины тупого угла.

Answer 1

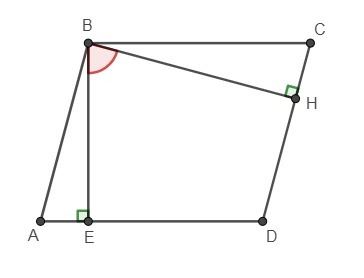
Очевидно, что в условии речь идет о соседних углах, так как противоположные углы параллелограмма равны.

∠ВАD = 5x

∠АВС = 7х

Сумма соседних углов параллелограмма равна 180°, тогда:

5х + 7х = 180

12х = 180

х = 15

∠ВАD = 5x = 5 * 15 = 75°

∠АВС = 7х = 7 * 15 = 105°

ΔАВЕ - прямоугольный

∠АВЕ = 90 - ∠ВАD = 90 - 75 = 15°

ΔВСН - прямоугольный

∠ВСН = ∠ВАD = 75° (противоположные углы параллелограмма равны)

∠СВН = 90 - ∠ВСН = 90 - 75 = 15°

∠ЕВН = ∠АВС - (∠АВЕ + ∠СВН) = 105 - (15 + 15) = 75°

Ответ: 75°

----------------------------------------------------------------------

Или так:

Острый угол равен 5х, тупой угол равен 7х, тогда:

5х + 7х = 180

12х = 180

х = 15

∠D = 7x = 7 * 15 = 105°

В четырехугольнике ЕВНD:

∠D = 105°;   ∠Е = ∠Н = 90°, тогда:

∠ЕВН = 360 - (105 + 90 + 90) = 75°

Ответ: 75°

---

Answer 2

task/29533363 Два угла параллелограмма относятся как 5: 7. Найдите угол между высотами параллелограмма, проведенными с вершины тупого угла.

Острый угол параллелограмма _∠A = 180°*5/(5+7) =75° ;  

Искомый угол= A (как углы со взаимно перпендикулярными сторонами ) .

Ответ: 75°

Comments

нужно рис. ?