g(x)
\medskip
\\
x^2>3
\medskip
\\
\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)>0
\medskip
\\
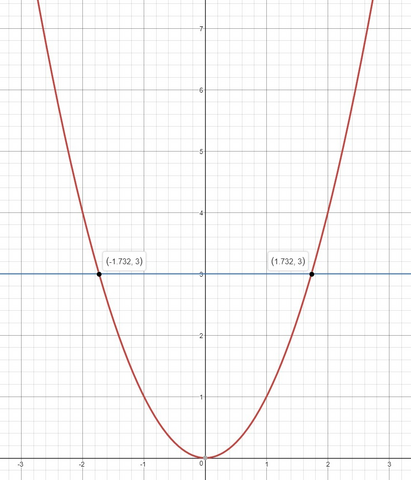
x\in\left(-\infty;-\sqrt{3}\right)\cup\left(\sqrt{3};+\infty\right)" alt="f(x)=x^2;~g(x)=3
\medskip
\\
1)~f(x)>g(x)
\medskip
\\
x^2>3
\medskip
\\
\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)>0
\medskip
\\
x\in\left(-\infty;-\sqrt{3}\right)\cup\left(\sqrt{3};+\infty\right)" align="absmiddle" class="latex-formula">
g(x)
\medskip
\\
x^2>3
\medskip
\\
\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)>0
\medskip
\\
x\in\left(-\infty;-\sqrt{3}\right)\cup\left(\sqrt{3};+\infty\right)" alt="f(x)=x^2;~g(x)=3
\medskip
\\
1)~f(x)>g(x)
\medskip
\\
x^2>3
\medskip
\\
\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)>0
\medskip
\\
x\in\left(-\infty;-\sqrt{3}\right)\cup\left(\sqrt{3};+\infty\right)" align="absmiddle" class="latex-formula">
Следовательно, все значения аргумента, что не входят в данный промежуток, будут лежать ниже прямой