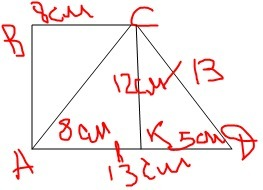
Дыагональ трапеції є бісектрисою тупого кута, а, як відомо, бісектриса трапеції відтинає від неї рівнобедрений трикутник (ΔАСД; АД = СД = 13 см).
З ΔСКД , де СК - висота трапеції, (∠СКД = 90°): СК = √(СД² - КД²), де КД = АД - АС = 13 - 8 = 5 см.
Отже, СК = √(13² - 5²) = √144 = 12 см, S = 0,5(BC + AD)·CK = 0,5(8 + 13)·12=
= 126 cм² .
Відповідь: 126 см².