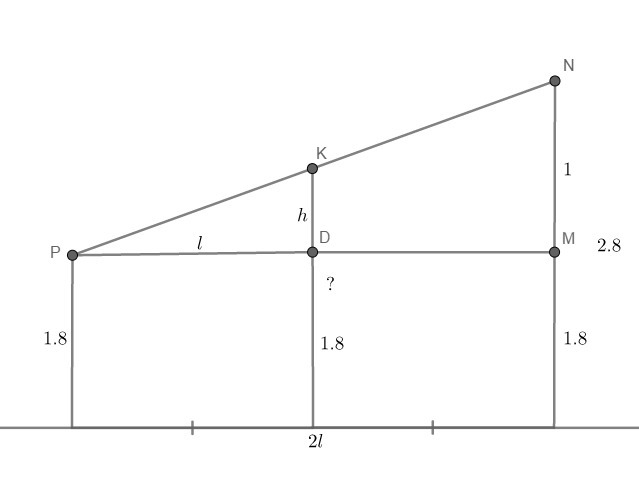
Проведем  , параллельную горизонтальной прямой. Получим
, параллельную горизонтальной прямой. Получим  .
.
Отсюда,

Высота средней опоры  м.
м.
По-другому можно было рассуждать так - поскольку средняя опора стоит посередине двух других, то её высота равна среднему арифметическому высот двух опор, находящихся по бокам от неё. Т.е., высота  м.
м.
Ответ.  м
м