a) 
Чтобы не рассматривать несколько случаев, когда (x-3)≥0 (x-3)≤0 , x≥0 , x≤0,возведём обе части равенства в квадрат, получим равносильное уравнение, т.к. обе части равенства неотрицательные.
|2x|\; \; \Rightarrow \; \; (x-3)^2>(2x)^2\\\\x^2-6x+9>4x^2\\\\3x^2+6x-9>0\\\\x^2+6x-9>0\; \; \Rightarrow \; \; (x+3)(x-1)>0\\\\znaki\; (x^2+6x-9):\; \; \; +++(-3)---(1)+++\\\\x\in (-\infty ,-3)\cup (1,+\infty )\; \; -\; \; otvet" alt="|x-3|^2=|2x|^2\\\\Tak\; kak\; \; a^2=|a|^2\; ,\; to\; \; (x-3)^2=(2x)^2\\\\x^2-6x+9=4x^2\\\\3x^2+6x-9=0\\\\x^2-2x-3=0\; \; \Rightarrow \; \; x_1=-3\; ,\; x_2=1\; \; \; (teorema\; Vieta)\\\\Otvet:\; \; x_1=-3\; ,\; x_2=1\; .\\\\2)\; \; |x-3|>|2x|\; \; \Rightarrow \; \; (x-3)^2>(2x)^2\\\\x^2-6x+9>4x^2\\\\3x^2+6x-9>0\\\\x^2+6x-9>0\; \; \Rightarrow \; \; (x+3)(x-1)>0\\\\znaki\; (x^2+6x-9):\; \; \; +++(-3)---(1)+++\\\\x\in (-\infty ,-3)\cup (1,+\infty )\; \; -\; \; otvet" align="absmiddle" class="latex-formula">
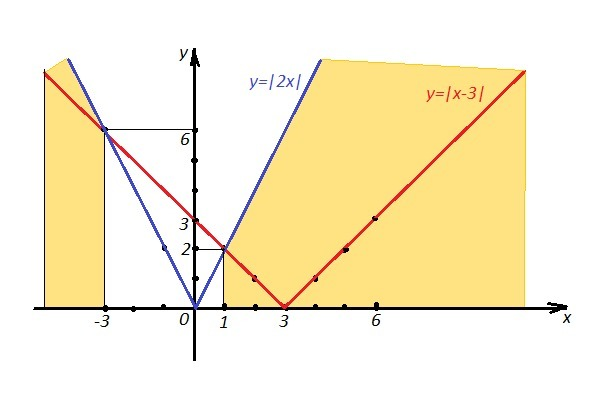
На рис. жёлтым цветом выделены части плоскости, где |x-3|<|2x| ( красный график функции y=|x-3| лежит ниже синего графика у=|2х| ).</p>
