координаты вершины (x₀; y₀) параболы y = ах² +bx +c

подставив х₀ в уравнение, находим у₀
26.1
y=x²+2
bx, в данном случае = 0
x₀= -0/2 = 0
y= 0²+2 = 2
y₀=2
(0;2)
26.2
y=-x²-5
x₀=0
y₀ = -5
(0;-5)
26.3
y=3x²+2x
x₀=-2/6=-1/3
y₀=3 (-1/3)²+2(-1/3) = 3/9 - 2/3 = 1/3 -2/3 = -1/3
(-1/3; -1/3)
26.4
y=-4x²+x
x₀=(-1)/(-8) = 1/8
y₀ = -4(1/8)² + 1/8 = -4/64 +1/8 = 1/16
(1/8; 1/16)
27. координаты этой точки- (х₀; 0)
1.
y= x²+3
x₀=0
(0;0)
2.
y=(x+2)² = x²+4x+4
x₀=-4/2 = -2
(-2;0)
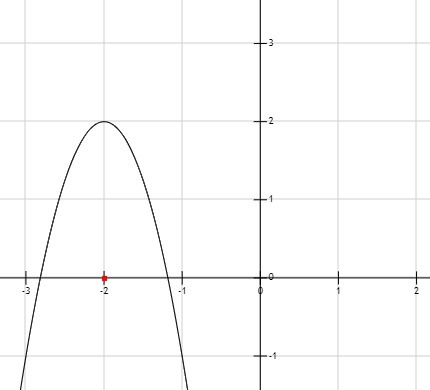
3.
y= -3(x+2)²+2 = -3(x²+4x+4)+2 = -3x² -12x-10 (см. график)
x₀=12/(-6) =-2
(-2;0)
4.
y=(x-2)²+2 = x²-4x+6
x₀=4/2 = 2
(2;0)
5.
y= x²+x+1
x₀=-1/2
(-1/2; 0)
6.
y= 2x²-3x+5
x₀=3/4
(3/4;0)