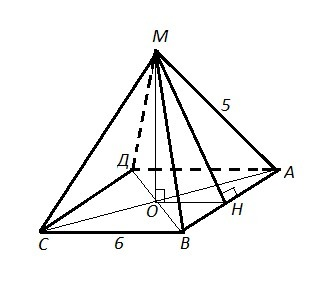
МАВСД - пирамида, АВСД - квадрат, АВ=ВС=СД=АД=6 см, МА=5 см.
Проведём МН⊥АВ, АН=НВ=6:2=3 см.
МН=√(МА²-АН²)=√(5²-3²)=4 см.
S(бок)=4·S(ΔАВМ)=4·(6·4:2)=4·12=48 (см²) .
МО⊥ пл. АВСД , МОН: ∠МОН=90° , ОН=ВС:2=6:2=3,
МО=√(МН²-ОН²)=√(4²-3²)=√7 (см)
V=1/3·S(АВСД)·МО=1/3·6²·√7=12√7 (см³).