Ответ:
Плоскость можно провести через две пересекающиеся прямые или через две параллельные прямые.
Через скрещивающиеся прямые плоскость провести нельзя.
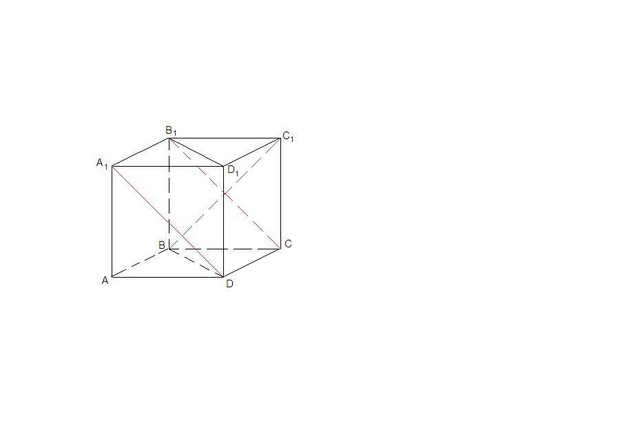
1) Да, так как прямые АВ и BD₁ имеют общую точку В, значит пересекаются.
2) Да, так ВВ₁ и DD₁ параллельны (ВВ₁║СС₁ и СС₁║DD₁ как противоположные стороны квадрата, значит ВВ₁║DD₁).
3) Нет, так как прямые АА₁ и BD₁ скрещивающиеся (АА₁ лежит в плоскости (AA₁D₁), BD₁ пересекает эту плоскость в точке D₁, не лежащей на АА₁).
4) Да, так как A₁D║B₁C. Рассмотрим четырехугольник A₁B₁CD: А₁В₁║CD (А₁В₁║C₁D₁, а C₁D₁║CD как противолежащие стороны квадратов), и
А₁В₁ = CD как ребра куба.
Тогда A₁B₁CD - параллелограмм, ⇒ A₁D║B₁C.
5) Нет, так как прямые АD и B₁C скрещивающиеся (АD лежит в плоскости (ABC), B₁C пересекает эту плоскость в точке C, не лежащей на АD).
Плоскость BDD₁ проходит через точку B₁. Точка В принадлежит плоскости BDD₁ и прямая DD₁ лежит в этой плоскости, значит прямая, проходящая через В параллельно DD₁ лежит в этой плоскости.