7)
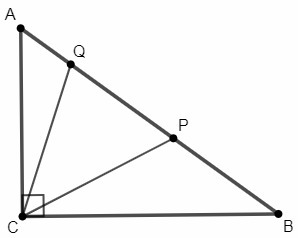
∠A+∠B=90° (сумма острых углов прямоугольного треугольника)
△ACP - равнобедренный: ∠CPQ=(180°-∠A)/2 =90° -∠A/2
Аналогично ∠CQP=90° -∠B/2
∠PCQ=180°-∠CPQ-∠CQP =
180°-(90° -∠A/2)-(90° -∠B/2) =
∠A/2 +∠B/2 =(∠A+∠B)/2 =90°/2 =45°
8)
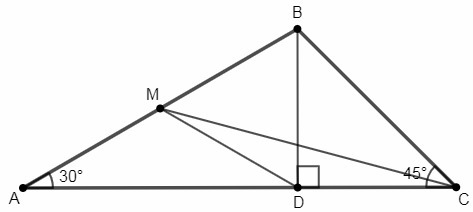
∠C=180°-30°-105° =45°
BD⊥AC
△BDC - равнобедренный (прямоугольный с углом 45°), BD=CD
BD=AB/2 (катет против угла 30° равен половине гипотенузы)
DM=AB/2 (медиана из прямого угла равна половине гипотенузы)
CD=BD=DM => △CDM - равнобедренный, ∠MCD=∠CMD
∠ADM=∠MCD+∠CMD =2∠MCD (внешний угол равен сумме внутренних, не смежных с ним)
△AMD - равнобедренный, ∠ADM=∠A=30°
∠MCD=∠ADM/2 =30°/2=15°