Преобразуем уравнение для того, чтобы решить относительно x.

Если любой отдельный множитель в левой части уравнения равен 0, то и все выражение будет равняться 0.


Приравняем первый множитель к 0 и решим.

Приравняем следующий множитель к 0 и решим.

Объединим решения.

Используем каждый корень для создания проверочных интервалов.



Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
 истинно
истинно
 ложно
ложно
 истинно
истинно
Решение включает все истинные интервалы:
 или
или 
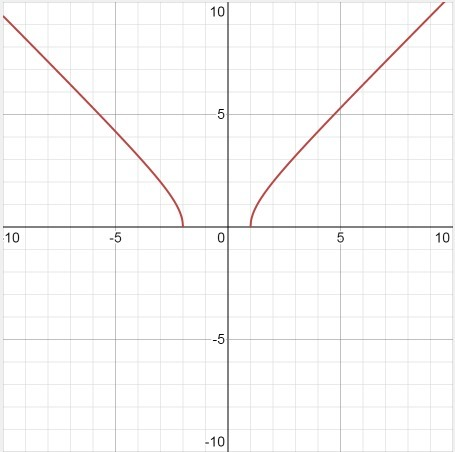
Областью определения являются все значения x, которые делают выражение определенным.
![(-\infty;-2]\cup [1;\infty) (-\infty;-2]\cup [1;\infty)](https://tex.z-dn.net/?f=%28-%5Cinfty%3B-2%5D%5Ccup%20%5B1%3B%5Cinfty%29)