Можно сразу сказать, что правильного ответа - не дано.
ДУМАЕМ - тело будет удаляться (r - возрастает) пока его скорость положительна (V > 0). Оно остановится и начнет возвращаться при t = 18 c, т.е. будет удаляться при t∈[0; 18]
РЕШЕНИЕ
Первый участок - равноускоренное движение.
Ускорение - а1 = 8/4 = 2 м/с², Vo=0 м/с - начальная скорость. t = 4 c.
Перемещение: r(2) = a*t²/2 = t² = 4² = 16 м (на 4 с) - путь на первом участке.
Скорость V(2) = 8 м/с - начальная скорость для второго участка.
Второй участок - равномерное движение со скоростью V = 8 м*с, а=0.
Время движения - t2 = 10 - 4 = 6 c
Перемещение (увеличивается):
r(10) = Ro + V*t2 = 16 + 8*6 = 64 м ( на 10 с) - второй участок.
Третий участок - равнозамедленное движение.
Ускорение торможения - а3 = (0 -8) : (18-10) = - 1 м/с².
Начальные данные: Ro = 64 м, Vo = 8 м/с, a = - 1 м/с², t = 8 c.
Перемещение по формуле
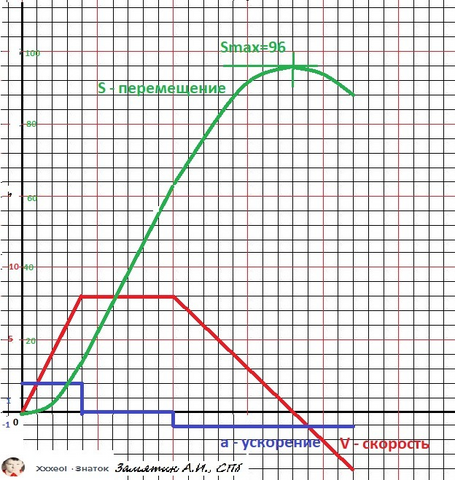
r(18) = 64 + 8*8 - (1/2)*8² = 64 +64 - 32 = 96 м - максимальное расстояние.
ОТВЕТ: t ∈(0 ; 18) - тело удаляется (расстояние увеличивается).
ДОПОЛНИТЕЛЬНО
Рассчитаем конечное положение тела при t = 22 c.(t3 = 12 c)
r(22) = 64 + 8*12 - (1/2)*12² = 64+96-72 = 88 м - конечная точка пути.
Рисунки с графиками всех трех функций - в приложении.
Еще одно подтверждение, что правильных ответов в списке - нет