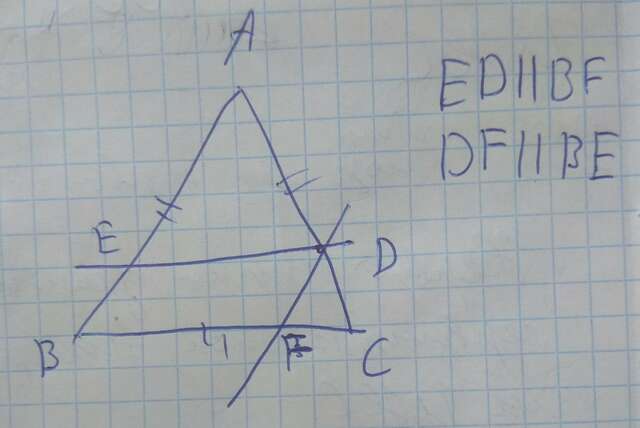
Получится параллелограмм (BEDF) . Углы 60, 60, 120, 120.
ED||BF по построению.
DF||EB по построению.
Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
У параллерограмма противоположные углы равны. Угол B равен 60°, т. к. это угол равностороннего треугольника (180 : 3 = 60). Угол EDF = B = 60.
Сумма углов четырехугольника равна 360°. BED = BFD. BED + BFD = 360 - EDF - B = 240
BED = BFD = 240 : 2 = 120.