Ответ:
2) 10 см
Объяснение:
1) Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
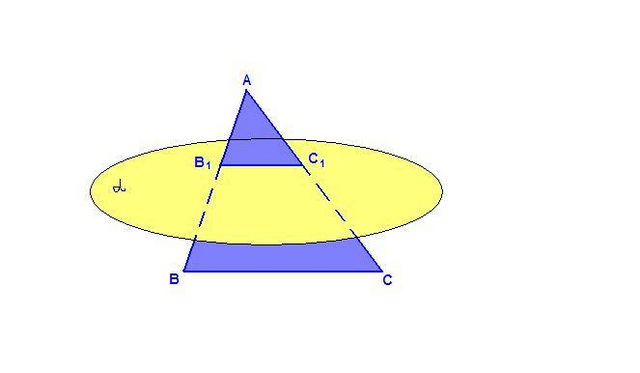
ВС ║ α, ВС ⊂ (АВС), (АВС) ∩ α = В₁С₁, ⇒
В₁С₁ ║ ВС.
2) По обобщенной теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки:
АВ : В₁В = АС : С₁С = 8 : 3
С₁С = 3 · АС / 8 = 3 · 16 / 8 = 6 см
АС₁ = АС - С₁С = 16 - 6 = 10 см