При х≥0
у=|х²-5х+6|
при х<0<br>у=|х²+5х+6|
график у=|f(x)|
y=f(x), f(x)≥0
y=-f(x), f(x)<0<br>поэтому у=|f(x)|
строится так
строим f(x) и ту часть , которая будет при у≥0 оставляем как есть,
а ту ,что при у<0 зеркально отражаем относительно ОХ <br>
поэтому построим функции под модулем
у=х²-5х+6=(х-3)(х-2)
у=0 х¹=2, х²=3 нули функции
х=0 у=6
ветви параболы вверх
у=х²+5х+6=(х+2)(х+3)
у=0 х¹=-2, х²=-3 нули функции
х=0 у=6
ветви параболы вверх
в общем виде наш график определяется так
при х≤-3
у=х²+5х+6
при -3<х≤-2<br>у= -х²-5х-6
при -2<х<0<br>у=х²+5х+6
при 0≤х<2<br>у=х²-5х+6
при 2≤х<3<br>у=-х²+5х-6
при х≥3
у=х²-5х+6
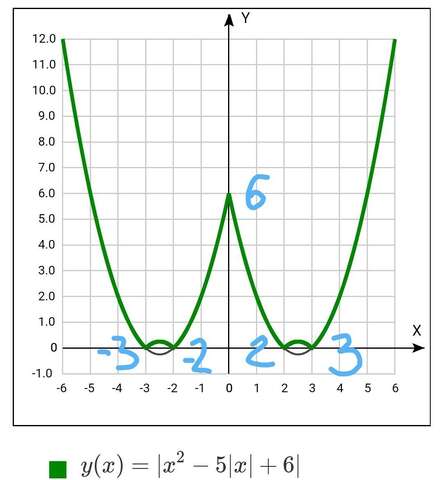
наш график построен
(Зелёная жирная линия)
PS
на самом деле можно было построить лишь часть графика , например при х≥0
а часть при х<0 получится зеркальным отражением построенного графика относительно ОУ<br>
потому что
у(х)=|х²-5|х|+6|=| |х|²-5|х|+6 |=у=( |х| )