Постройте график функции. Укажите область определения, множество значений, промежутки...

Question

Дан 1 ответ

spasibo3pajbrh_zn · Answer 1 · 2020-05-17T19:45:25+0000

$y (x)= |2 - \sqrt{5 + |x| } | \\$
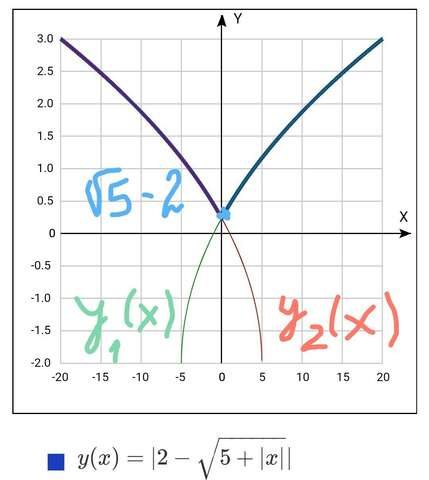
областью определения y(x) будет x€R
(5+|x|>0 при любых x)

Теперь найдем множество значений, исходя из свойств модуля и квадратного корня
$|x| \geqslant 0$
$5 + |x | \geqslant 5$
$\sqrt{5} \geqslant \sqrt{5 + |x| } \geqslant 0$
$2 - \sqrt{5 + |x|} \leqslant 2 - \sqrt{5}$

0" alt=" y(x) = |2 - \sqrt{5 + |x|} | \geqslant \\ \geqslant | 2 - \sqrt{5} | = \sqrt{5} - 2 > 0" align="absmiddle" class="latex-formula">
как мы видим нулей функции у(х) нет

теперь раскроем внутренний модуль,
а затем внешний

$y (x)= |2 - \sqrt{5 + |x| } | \\ = \left \{ |{ 2 - \sqrt{5 + x} |} , x \geqslant 0 \atop |{2 - \sqrt{5 - x} | , \: x < 0} \right. = \\ = \left \{ { - 2 + \sqrt{5 + x} } , x \geqslant 0 \atop { - 2 + \sqrt{5 - x} , \: x < 0} \right.$

внешний модуль раскрывается основываясь на сравнении значения квадратного корня и 2 при значениях х из заданных интервалов.

из вида функции и свойств квадратного корня мы видим , что
при х>0 функция возрастает
при х<0 функция убывает<br>

причём минимум функции будет при х=0

$y (0)= |2 - \sqrt{5 + |0| } | = \\ = \sqrt{5} - 2 \\$

Функции , составляющие y(x)

$y_1 = { - 2 + \sqrt{5 + x}} \\ y_2 = { - 2 + \sqrt{5 - x}}$
строятся на основе функции
$\sqrt{x}$
соответствующими сдвигами вдоль осей ординат и абсцисс

Финальный график - см на фото

удачи!